大数の法則と中心極限定理の歴史
確率論の発展を変えた重要な発見とその背景
私たちの身の回りにある多くの自然現象や社会現象は、ある特定のパターンに従っています。その中でも「大数の法則」と「中心極限定理」は特に重要で、これらは今日の統計学、科学、金融、保険など多くの分野の基礎となっています。これらの重要な法則はどのようにして発見されたのでしょうか?ここでは、数学史上の重要な発見とその背景について、初心者の方にもわかりやすく解説します。
大数の法則の発見
大数の法則の発見のきっかけ
ベルヌーイが大数の法則に興味を持ったのには、いくつかの理由がありました:
- 17世紀後半は、ギャンブルや賭けに関する確率問題が盛んに議論されていました
- パスカルとフェルマーの確率に関する手紙や、ホイヘンスの初期の確率論に影響を受けました
- 実用面では、当時発展しつつあった保険や年金制度の計算基盤を提供したいという思いもありました
ベルヌーイは「同一条件下での繰り返し試行において、結果の頻度が理論的確率にどう近づくか」という問いを解明しようとしました。彼の発見は後に「弱法則」と呼ばれ、20世紀になってボレルやコルモゴロフによってさらに発展した「強法則」が証明されました。
中心極限定理の発見と発展
ラプラスと天文学の物語
ラプラスが中心極限定理に取り組むきっかけとなったのは、彼の天文学者としての仕事でした。18世紀末から19世紀初頭、天文学者たちは惑星や天体の位置を正確に測定しようと努力していましたが、観測には常に誤差が伴っていました。
彼は宮廷天文学者として、土星と木星の軌道の「不規則性」を研究していました。同じ天体を複数回観測すると結果が少しずつ異なるため、測定誤差と本当の軌道変化を区別する必要がありました。
多くの観測データを分析する中で、ラプラスは測定誤差に興味深いパターンがあることに気づきました:
- 小さな誤差は頻繁に発生する
- 大きな誤差はまれにしか起こらない
- 誤差の分布が「釣鐘型」になる
ラプラスとナポレオンとの間には有名なエピソードがあります。ナポレオンが彼の著書について「神への言及がない」と指摘したとき、ラプラスは「陛下、その仮説は必要ありませんでした」と答えたと伝えられています。
ガウスと小惑星ケレスの物語
1801年、イタリアの天文学者ピアッツィが小惑星ケレスを発見しましたが、わずかな観測後に見失ってしまいました。ガウスは限られた観測データから小惑星ケレスの軌道を予測するという課題に取り組みました。
彼は観測誤差の処理方法を研究する中で、次のような洞察を得ました:
- 小さな誤差は大きな誤差より頻繁に発生する
- 正の誤差と負の誤差は同じ確率で発生する
- 多くの独立した小さな誤差が組み合わさると、ある特定の数学的分布に従う
ガウスの計算に基づき、ケレスは1801年12月31日に再発見されました。これは彼の方法の正確さを証明し、一躍有名になりました。彼の予測は、天文学者オルバースが望遠鏡を向けるべき空のごく小さな領域を特定するほど正確でした。
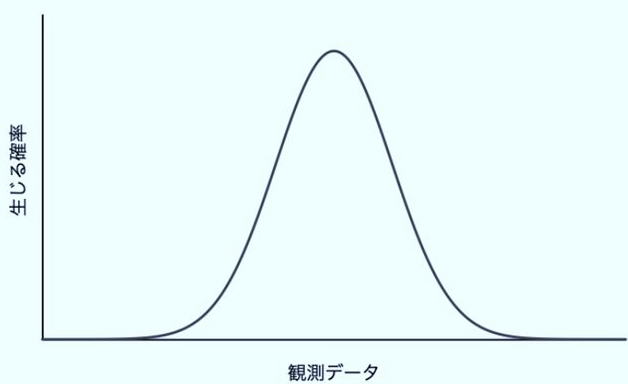
正規分布(ガウス分布)のグラフ:中央に集中し、両端に向かって対称的に減少する釣鐘型の曲線
なぜ数学者たちは天文観測に熱中したのか?
17〜19世紀の数学者たちが天文観測に熱中した理由はいくつかあります:
- 宇宙の謎を解きたかった:星や惑星の動きは大きな謎であり、宇宙の法則を見つけるために空を観察していました。
- 航海のために必要だった:船の航海では星の位置を知ることが不可欠で、星の正確な位置の測定は重要な仕事でした。
- カレンダーや時計の作成:星の動きから1年の長さや季節の変わり目を知り、より正確なカレンダーを作成していました。
- 数学を応用できる場所:天文学は複雑な計算が必要で、数学者の能力を発揮できる最高の場でした。
- 職業としての天文学:多くの数学者が天文台で働いていました。例えばガウスはゲッティンゲン天文台の台長を務めました。
- 社会的地位:天文学者は社会的に尊敬される地位にありました。
小学生にもわかる星と誤差の話
むかしむかし、とても頭のいい人たちがいました。ガウスさんとラプラスさんという、すごい数学者です。彼らは星を見るのが大好きでした。でも、星の場所や明るさを正確に測るのはとっても難しかったんです。
同じ星を何回も測ると、答えがいつも少しずつ違ってしまいます。これを「誤差(ごさ)」と言います。ある日、彼らは気づきました。たくさんの測定結果を紙に書いていると、面白いことが見えてきたのです。
「あれ?小さな間違いはたくさんあるけど、大きな間違いは少ないぞ。そして、その分布が...ベルの形になっている!」
例えば、星の場所を100回測って、本当の場所からどれだけずれているかを調べると:
- ほんの少しだけずれたもの → たくさんある(真ん中が高い)
- かなりずれたもの → 少ない(両端が低い)
- 真ん中を頂点として、両側に広がる山のような形になる
これを理解するために、こんなゲームを考えてみましょう:30人の友だちに目隠しをして、的当てゲームをやってもらいます。みんな的の中心を狙っているけど、少しずつ違う場所に当たります。終わった後、矢が刺さった場所を見ると...なんと!真ん中に一番多く集まって、端に行くほど少なくなる「山」の形になりました。
この発見のおかげで、私たちは少ない測定から、より正確な答えを予測できるようになりました。ガウスさんはこの発見を使って、見失った小さな星(小惑星ケレス)を再発見することができました。「こっちの方向を見てみて!」と計算したら、本当にそこに星があったのです!
現代での応用例
統計学と科学研究
大数の法則と中心極限定理は、科学実験のデータ分析の基礎となっています。多くの測定を行い、平均値を取ることで、より正確な結果が得られることの理論的根拠になっています。
金融と投資
投資理論では、分散投資の効果を説明するのに大数の法則が用いられます。また、リスク評価やオプション価格の計算には正規分布が広く使われています。
保険数理
保険会社は大数の法則に基づいて保険料を計算します。多くの加入者がいれば、全体の保険金支払いは予測可能になるという原理です。
品質管理
製造業では、製品の品質管理に正規分布が利用されます。測定値が正規分布に従うという前提で、許容範囲や検査方法が決められています。




